Geometry representations play a crucial role in solving complex 3D vision problems. The rapid evolution of deep learning has sparked significant interest in developing neural network-compatible geometric data representations. Recent technological advances, particularly those centered on coordinate networks, have demonstrated promising capabilities in modeling 3D geometry across diverse applications. These coordinate networks offer a functional approach that integrates seamlessly with neural network architectures. However, existing methodologies encounter substantial challenges, including limited accuracy in capturing intricate geometric structures and significant difficulties processing non-watertight objects. These limitations have prompted researchers to explore innovative approaches that can more comprehensively represent geometric information across different topological configurations and structural complexities.
Geometric data representations encompass various techniques, each presenting unique strengths and inherent limitations in 3D vision applications. Triangle and polygonal meshes, traditionally employed in geometry processing, demonstrate significant drawbacks due to their inconsistent data structures when handling shapes with variable vertex counts and connectivity. Voxel-based representations, while advantageous for learning-based tasks, impose substantial memory constraints, particularly when high-resolution details require comprehensive capturing. Point clouds, readily obtainable from sensor technologies, are extensively utilized in geometric learning but suffer from potential information loss and reduced expressiveness. Their effectiveness critically depends on sampling density and uniformity, with inherent challenges in defining surface structures, boundaries, and complex geometric relationships. These limitations underscore the necessity for more adaptive and versatile geometric representation methodologies.
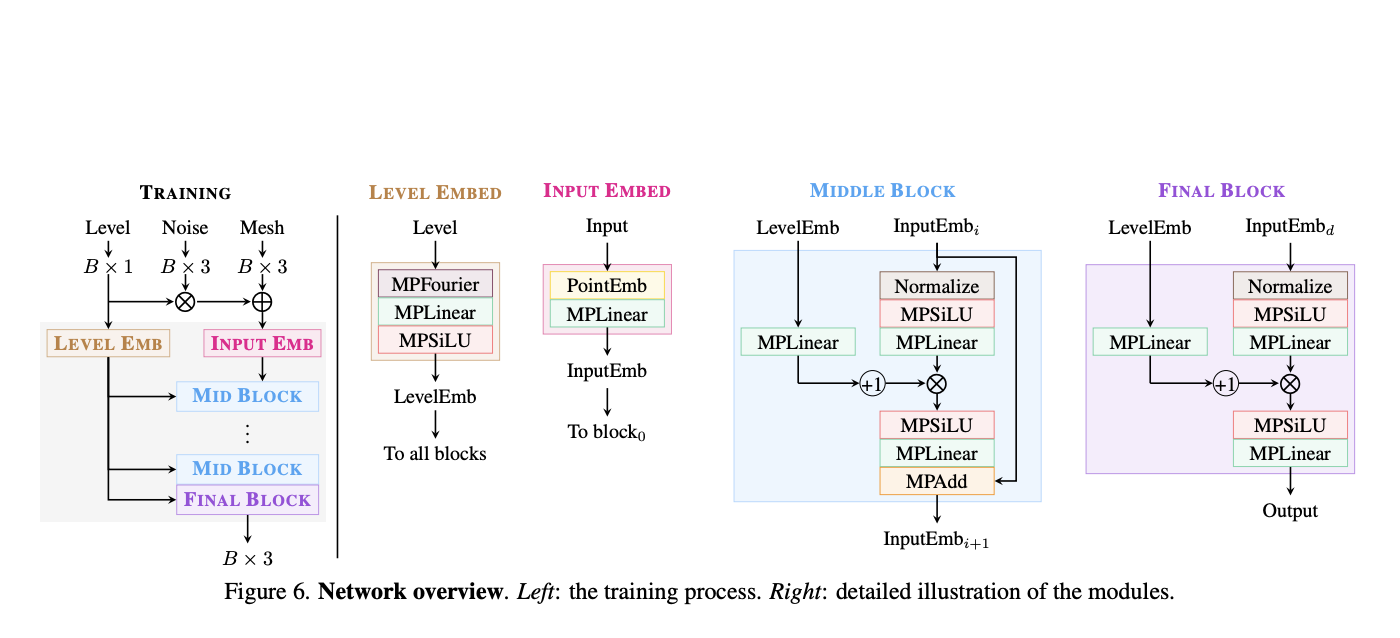
Researchers introduce GEOMETRY DISTRIBUTIONS (GEOMDIST), an innovative geometric data representation using a sophisticated diffusion model with a robust network architecture. By solving a forward ordinary differential equation (ODE), the approach transforms spatial points sampled from Gaussian noise space into precise surface points within shape space. This methodology enables the generation of an infinite point set for geometry representation, facilitating uniform surface sampling compared to existing vector field-based formulations. The approach also develops a backward ODE algorithm, permitting inverse mapping from shape space to noise space. GEOMDIST demonstrates remarkable accuracy and robustness across diverse complex structural configurations. Importantly, the representation simultaneously supports encoding texture and motion information alongside geometric data, presenting a versatile and compact neural representation of 3D geometry with significant potential for advanced applications.
GEOMDIST introduces an innovative approach to modeling surfaces as probability distributions, aiming to represent geometric structures with unprecedented flexibility. The method transforms surfaces into a probability distribution ΦM, where every sampled point corresponds precisely to the surface. Inspired by “Geometry Images”, this representation utilizes diffusion models to map Gaussian distributions to surface point distributions. Unlike existing techniques focused on shape synthesis, GEOMDIST concentrates on shape representation itself. The researchers developed a sophisticated network design that addresses the limitations of previous coordinate-based networks, which struggled to capture detailed geometric features. By standardizing layer inputs and outputs and implementing a dynamic resampling strategy, the approach simulates an effectively infinite number of surface points, approximating underlying geometric structures with remarkable precision and adaptability.
GEOMDIST demonstrates remarkable versatility in representing 3D surfaces through multiple innovative applications. The approach enables natural surface sampling at any desired resolution without computational overhead, eliminating the need for storing high-resolution point clouds. By training a compact network that retains comprehensive geometric information, researchers can generate surface points dynamically for specific use cases. The method proves particularly effective in handling complex scenarios, such as non-watertight surfaces that challenge traditional implicit function-based representations. In addition, the approach extends beyond pure geometry, incorporating additional information like texture colors and motion. Experimental results showcase the technique’s ability to reconstruct surfaces at varying resolutions, generate Gaussian splatting for novel view synthesis, and even represent dynamic geometries by introducing temporal inputs to the denoiser network. These capabilities highlight GEOMDIST’s potential to revolutionize geometric data representation.
This study introduces GEOMDIST, representing a significant breakthrough in geometric data representation, effectively addressing critical limitations inherent in traditional methodologies. By modeling 3D surfaces as geometry distributions within a sophisticated diffusion model framework, the approach transcends conventional constraints related to watertightness and manifold requirements. The technique enables flexible and precise sampling across complex geometric structures, demonstrating unprecedented adaptability in neural 3D representation techniques. Researchers have established a robust foundation for future exploration in geometry modeling, processing, and analysis. This innovative approach not only overcomes existing technological barriers but also opens new pathways for understanding and manipulating geometric data with greater precision and computational efficiency.
Check out the Paper and Project Page. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 59k+ ML SubReddit.
Asjad is an intern consultant at Marktechpost. He is persuing B.Tech in mechanical engineering at the Indian Institute of Technology, Kharagpur. Asjad is a Machine learning and deep learning enthusiast who is always researching the applications of machine learning in healthcare.
